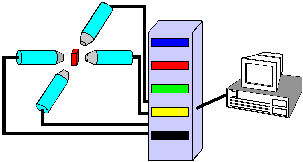
In der nuklearen Festkörperphysik werden — wie der Name schon sagt — kernphysikalische Messmethoden benutzt, um Eigenschaften von Festkörpern zu untersuchen. Eine bewährte Methode neben beispielsweise dem Mößbauer-Effekt, der Magnetischen Kernresonanz (Nuclear Magnetic Resonance, NMR), der Rutherford- Rückstreuung (Rutherford Backscattering, RBS) oder der Positronenvernichtung ist die gestörte γ-γ-Winkelkorrelation (Perturbed Angular Correlation, PAC), bei der man radioaktive Sonden in einem Festkörper einbringt, um dann, anhand ihrer Gamma-Ausstrahlcharakteristik, Kristallfelder zu untersuchen. Es werden Sonden benutzt, bei deren Zerfall im Tochterkern eine γ-γ-Kaskade bevölkert wird. Der Zwischenzustand der Kaskade (isomeres Niveau) darf keine zu lange Lebensdauer besitzen, weil dann der Untergrund durch zufällige Koinzidenzen in den aufgenommenen Spektren dominiert. Andererseits ist die Lebensdauer nach unten hin durch die Zeitauflösung der Apparatur begrenzt.
 |
Das generelle Ziel ist es, die Anwesenheit sowie das Verhalten von Störstellen (Fremdatome, Leerstellen) in Halbleitern wie Silizium, Germanium, Galliumarsenid, Indiumphosphid u.a. zu untersuchen.
Dazu wird ein geeignetes radioaktives Atom, ein Spion sozusagen, genannt Sondenatom, in ausreichender Zahl (typisch 1012) in den zu untersuchenden Festkörper, im PAC-Sprachgebrauch auch Probe genannt, eingebaut.
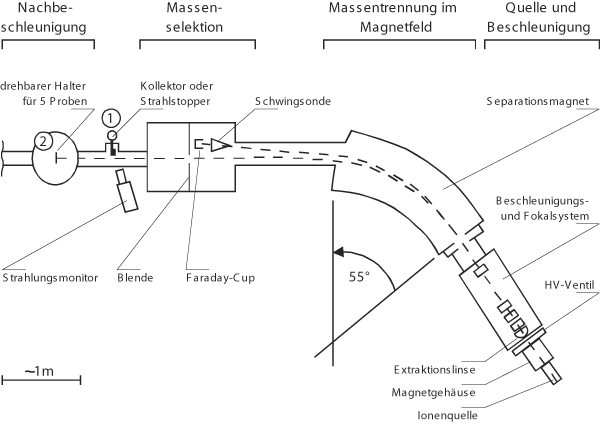
Die gängigen PAC-Sondenatome sind 111In, 181Hf und inzwischen auch 77Br. Der Einbau der radioaktiven Sondenatome in den Festkörper kann durch direkte Implantation, durch Rückstoßimplantation oder durch chemische Methoden erfolgen. In Bonn werden der Bonner Isotopenseparator zur direkten Implantation und das Bonner Zyklotron zur Rückstoßimplantation benützt.
 |
Da es bei der Implantation von Atomen in einen Festkörper zur einer Zerstörung der Kristallstruktur kommt, ist danach noch die Anwendung eines Ausheilverfahrens nötig. Dabei wird die Probe so erhitzt, dass sich die zerstörte Kristallstruktur reorganisiert und sich das Kristallgitter wieder aufbaut (Annealing).
Das Sondenatom befindet sich nun idealerweise fest eingebaut in dem Kristallgitter der Probe. Die elektrische Ladungsverteilung der umgebenden Gitteratome erzeugt am Ort des Sondenatoms einen elektrischen Feldgradienten (EFG). Ist die Umgebung um das Sondenatom von hoher (kubischer) Symmetrie, wie dieses z.B. in einem Silizium- oder Germaniumkristall (Diamantgitter) der Fall ist, so ist dieser EFG am Ort des Sondenatoms gleich Null, da sich alle Anteile gegenseitig aufheben: Das Sondenatom ist ungestört!
 |
Kommt nun ein Defekt in die Nähe eines Sondenatoms, so zerstört seine Anwesenheit die Symmetrie in der Umgebung des Sondenatoms. Jetzt ist der resultierende EFG am Ort des Sondenatoms nicht mehr Null. Das Sondenatom ist gestört!
 |
 |
Aufgrund der bereits angedeuteten besonderen Eigenschaften des Sondenatoms kann man diese Störung quantitativ messen und somit auswerten. Was sind aber nun die besonderen Eigenschaften des Sondenatoms und wie genau kann man die Störung messen?
Einerseits ist es notwendig, dass das Sondenatom über eine γ-γ-Kaskade zerfällt. Andererseits muss das Zwischenniveau dieser Kaskade zum einen ein genügend großes Quadrupolmoment Q besitzen, und zum anderen eine ausreichend lange Halbwertszeit t1/2 aufweisen.
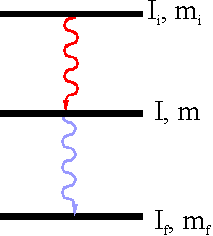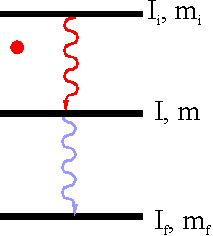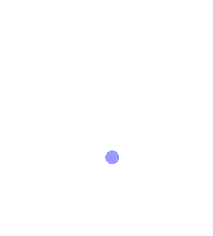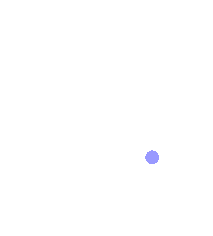 |
Nach der Emission des ersten γ-Quants befindet sich der Kern des Sondenatoms im Zwischenzustand der Kaskade. Nun gibt es aus Gründen der Spinerhaltung bzgl. der Emissionsrichtung des ersten Gammas eine räumliche Wahrscheinlichkeitsverteilung für die Emissionsrichtung des zweiten Gamma-Quants. Für verschiedene Winkel zwischen den Emissionsrichtungen von γ1 zu γ2 gibt es also verschiedene Wahrscheinlichkeiten. Daher spricht man von Winkelkorrelation.
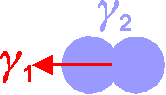
Anschaulich kann man sich die Emissionswahrscheinlichkeit des γ2 bzgl. γ1 im einfachsten nichttrivialen Fall als eine Keule vorstellen, die sogenannte Emissionskeule.
 |
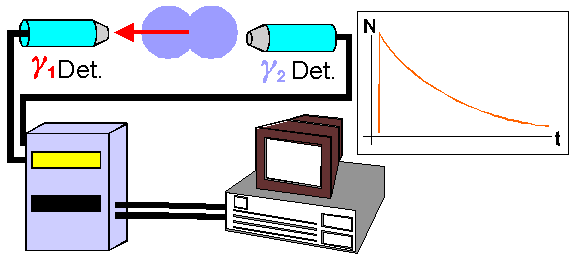
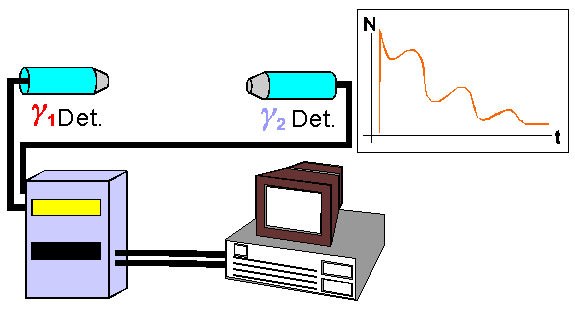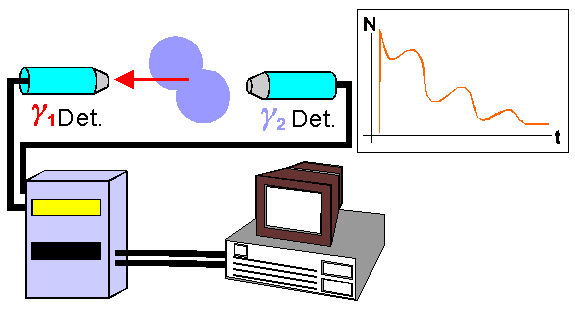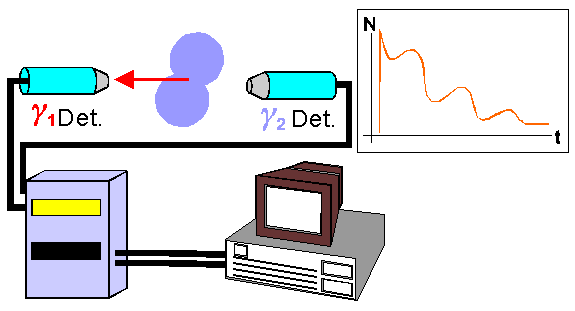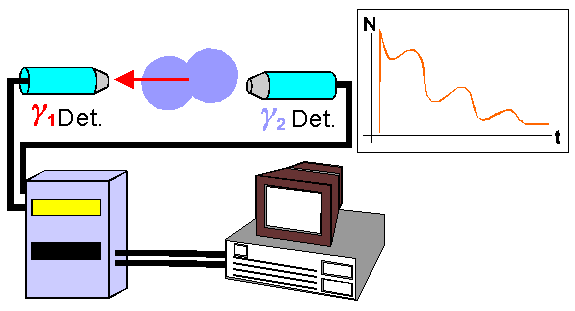
Wirkt auf den Spin des Sondentoms, während es sich im Zwischenzustand befindet, kein EFG (oder magnetisches Moment) ein, bleibt diese Emissionskeule mit der Zeit stabil. In diesem Fall handelt es sich um eine ungestörte Winkelkorrelation. Mit zwei γ-Detektoren, von den der eine nur γ1 und der andere nur γ2-Teilchen meldet, und die an eine Koinzidenzschaltung gekoppelt sind, die auch noch die Zeit zwischen dem Ansprechen des ersten und des zweiten Detektors aufnimmt, kann man dann die exponentiell abfallende Lebensdauerkurve des Zwischenniveaus sehen.
 |
Nun wirkt jedoch auf den Spin des Sondenatoms, während es sich im Zwischenzustand befindet, ein EFG ein. Aufgrund der Wechselwirkung zwischen dem EFG und dem Quadrupolmoment Q kommt es zu einer Präzession (Kreiselbewegung) des Kernspins im Zwischenniveau und somit wird auch die Emissionskeule mit der Zeit gedreht, sie kreiselt. In diesem Fall handelt es sich um die gestörte Winkelkorrelation, oder eben PAC. Bei Verwendung derselben Detektorkombination wie oben sieht man dann diese Kreiselbewegung als eine Modulation der Lebensdauerkurve mit eben der Kreiselfrequenz.
 |
Da gilt, dass die Kreiselfrequenz proportional zum EFG ist, kann man (bei bekanntem Quadrupolmoment Q) aus der Messung der Frequenz den EFG errechnen.
Um nun die Frequenz besonders gut messen zu können, und um neben der Größe des EFG's auch seine Orientierung, also seine räumliche Lage bestimmen zu können, benutzt man nun nicht nur zwei, sondern eine Kombination aus 3, 4 oder noch mehr Detektoren mit dazugehöriger Koinzidenzelektronik. Außerdem kann man durch die Verrechnung mehrer Koinzidenzspektren, wie sie in Abbildung 9 zu sehen sind, die Lebensdauerkurve eleminieren.
Der so gemessene elektrische Feldgradient (Größe und Lage) wird dann benutzt, um theoretische Kalkulationen über die Lage von Gitterdefekten zu überprüfen. Weiterhin kann bei den verschiedenen Versuchen die Temperatur der Probe, die Stärke der Dotierung mit Fremdatomen und ähnliches variiert werden. Über die Beobachtung der Auswirkungen auf den EFG, die sich beim Verändern dieser Parameter ergeben, kann dann ebenfalls auf die Natur des Defektes geschlossen werden.
