The perturbed angular correlation method

The technique of the perturbed angular correlation (PAC) belongs to the class of hyperfine spectroscopic methods as the Mößbauer-spectroscopy. The hyperfine interaction between the electromagnetic moments of the nuclear state and the external electromagnetic fields at nuclear site is measured. This technique can be used for determine the magnetic dipole and the electric quadrupole moments of the nuclear states and using nuclei with known moments for deriving the internal electromagnetic fields in solids, liquids, gases, ions and free atoms.

So the perturbed angular correlation started with being a technique used in nuclear physics, measuring spins and parities. With the development of the experimental techniques the angular correlation was recognised having a high potential in condensed matter research and today its applications are predominantly in this area.

The principle of perturbed angular correlation consists in producing a radioactive nuclei that decays over a γγ-cascade in the ground state of the daughter nucleus and to bring it into the host material under research. The initial state with nuclear spin |I_i, m_i〉 decays (see figure 1) through the emission of a γ-quant γ₁ in an interstitial state |I_s, m_s〉 and this under emission of a second γ-quant γ₂ in the final state or ground state |I_f, m_f〉.

**Figure 1:** Schematic illustration of a γ-γ-cascade

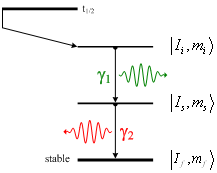The emission of the first γ is isotropic. Detecting γ₁ in a fixed direction →k₁ an ensemble of nuclei with oriented spins is selected. This produces an unequal (inhomogeneous) population of the m-states of the intermediate state. The detecting of the succeeding radiation in the direction of →k₂ is not isotropic anymore and shows a definite angular correlation with respect to the first.

The aim is to find the relative probability W(ϑ)dΩ of detecting γ₂ in the solid angle dΩ with the angle ϑ in respect to γ₁. This probability is given by the angular correlation function

W(ϑ) =

k_max
∑
k

A_kkP_k(cosϑ)

(1)

For a γγ-cascade is k even because of the conservation of parity and 0 < k < min(2I_s, l_i+l′_i). Here is I_s the spin of the interstitial state and l_i with i=1;2 the multipolarities of the two transitions. For pure multipole transitions l_i=l′_i. The parameters A_kk are the so called angular correlation coefficients and are depending of the angular momenta of the state and the multipolarities of the transitions.

The radioactive nuclei, decaying through a succession of two γ-radiations, are often built in materials that have to be investigated. Here the probe nucleus can be perturbed during the finite lifetime of the intermediate state from the hyperfine interaction of magnetic or electric surroundings. Through this perturbation the angular correlation function is changing to

W(ϑ) =

k_max
∑
k

A_kkG_kk

(2)

where G_kk is the perturbation factor containing the information about the interaction. Both the magnetic and the electric interaction exercise a torque on the angular momentum of the intermediate state which produces a precession of →I_s around the symmetry axis. Quantum mechanically this means that the interaction can lead to transitions among the m-states. So the second radiation is emitted from a level with an altered population distribution and this change is responsible for the attenuation of the correlation. The interaction can occur between the nuclear magnetic dipole moment →μ of the intermediate state →I_s and the extranuclear magnetic field →B or between the nuclear electric quadrupole moment Q and the extranuclear electric field gradient V = ∇²Φ.

Magnetic hyperfine interactions

For magnetic hyperfine interactions the frequency of the precession of the nuclear spin around the axis of the magnetic field →B is the Larmor-frequency

ω_L = −

g μ_N B

(3)

where g is the g-factor (Landé-factor) of the intermediate state and μ_N the nuclear magneton (μ_N=5.05·10⁻²⁴ [(erg)/(G)]=5.05·10⁻²⁷ [(J)/(T)])¹.

The precession involve a rotation of the intensity distribution of the γγ-cascade and the coincidence counting rate is subject to a modulation. Quantum mechanically the magnetic hyperfine interaction splits the intermediate state into |2I+1| equidistant sublevels. The energy difference between the sublevels is

∆E = ħ ω_L = −g μ_N B

(4)

From the measurement of the Larmor-frequency it is possible to determine either the g-factor or the magnetic field, depending on which quantity is known.

Static electric hyperfine interactions

Historically the technique of the perturbed angular correlation was used to measure the magnetic moments of excited nuclei and less for determine the electric quadrupole moments. The problem hereby was, that also with the strongest external electric field gradients the quadrupole hyperfine interaction was too small to be measured with known methods. Electric fiel gradient that are strong enough to be measured are found in non-cubic solids and non complete electron shells.

The energy of the electric hyperfine interaction between the charge distribution of the nucleus and the extranuclear static electric field can be expanded into mutlipoles. The monopole term solely causes an energy shift and the dipole term vanishes, so the first relevant expansion term is the quadrupole term

E_Q =

∑
ij

Q_ijV_ij i,j = 1;2;3

(5)

which can be written as the product of the quadrupole moment Q_ij and the electric field gradient V_ij. Both are tensors of the second order. Higher term of the expansion are too small to be detected with PAC.

The electric field gradient is the second derivate of the electric potential at nuclear site

V_ij =

∂²φ(0)

∂x_i ∂x_j

(6)

Through adequate principle axis representation it is possible to diagonalise V_ij so that

|V_zz| ≥ | V_yy| ≥ |V_xx|

Because of the Laplace equation, ∑_ijV_ij=0, only two of the three components V_ii are linear independent. Usually the largest component V_zz and the asymmetry parameter η, defined as

η: =

V_yy − V_xx

V_zz

(7)

are chosen to characterise the electric field gradient.

For cubic crystals, which are equivalent in all directions x, y and z (therefore V_zz = V_yy = V_xx) and also for axially symmetric crystals, which are equivalent in x and y (therefore V_yy = V_xx) the asymmetry parameter vanishes η = 0. In cases of smaller symmetry η takes values between zero and one.

For axially symmetric electric field gradients the energy of the sublevels takes the values

E_Q =

e Q V_zz

4I(2I−1)

·( 3m² − I(I+1) )

(8)

The energy difference between two sublevels m and m′ is given by

∆E_Q = E_m − E_m′ =

e Q V_zz

4I(2I−1)

·3 |m² − m′²|

(9)

After introducing the quadrupole frequency

ω_Q : =

e Q V_zz

4I(2I−1) ħ

(10)

for the energy difference can be written

∆E_Q = ħ ω_Q ·3 |m² − m′²|

(11)

In contrast to the magnetic interaction the splitting of the sublevels of the nuclear state through the electric quadrupole interaction depends on the angular moment →I of the sublevel and is therefore non-equidistant. The transitions frequencies ω_n between the different sublevels are, in case of η = 0, integer multiples of the smallest frequency ω₀. It can be written

ω_n = n ·ω₀

where

ω₀ : = min

⎛
⎝

·∆E_Q

⎞
⎠

whereas ω₀ = 3 · ω_Q for integer nuclear spin I and ω₀ = 6 · ω_Q for half integer nuclear spin I.

As for the magnetic dipole interaction, also the electric quadrupole interaction induces a precession of the angular correlation in time and this modulates the quadrupole interaction frequency. This frequency is an overlapping of the different transition frequencies ω_n. The relative amplitudes of the different components depend on the orientation of the electric field gradient relative to the detectors (symmetry axis) and on the asymmetry parameter η. For a study with different nuclei one needs a parameter that allows a direct comparison, therefore the interaction frequency ν_Q is introduced, which is independent from the nuclear spin →I.

ν_Q : =

e Q V_zz

(12)

Experimental setup

There are two different ways of measuring the angular correlation, the time integral and the time differential mode. The integral perturbed angular correlation (IPAC) is used if the lifetime of the intermediate state is smaller or similar to the experimental time resolution or for measuring strong internal magnetic fields of ferro magnets. The time differential perturbed angular correlation (TDPAC) measures the angular correlation as fraction of the time the nucleus spends in the intermediate state.

**Figure 2:** Setup of an fast-slow-coincidence circuit

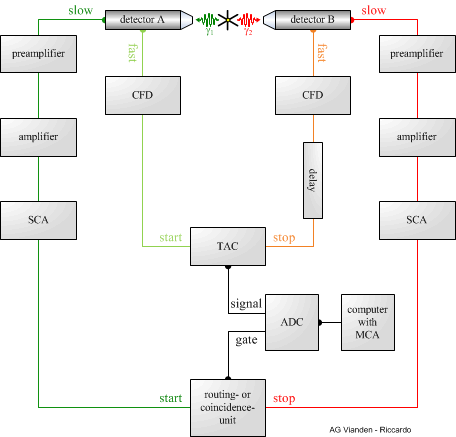Experimentally the number of coincident events between γ₁ and γ₂ is measured as a function of time. In a simple experimental setup (as shown in figure 2) the probe is put between two scintillation detectors which are connected to a fast-slow-coincidence circuit, so two signals are derived from each detector: the fast timing signal and the slow energy pulse. The fast timing signal is fed into the time-to-amplitude converter (TAC), an electronic clock, which allows to measure the time the nucleus spent in the intermediate state of the cascade. The TAC is started by the fast signal of the first detector and stopped by that of the second detector. Its output amplitude is than proportional to the time between the two signals-pulses. To assure that the TAC is started by the signal of γ₁ and stopped by that of γ₂ the slow output of the detectors, which is proportional to the energy of the incoming and detected radiation, is used. The right energy is chosen by setting the windows of the single channel analysers (SCA) whose output gates the multichannel analyser (MCA). This electronic device sorts the incoming signals by their amplitude in channels. Usually setups with more than two detectors are chosen so that the coincident counting rate increases and the time for achieving a reasonable statistic decreases. In the literature setups using up to eight detectors are reported; here a setup consisting of four detectors is used.

Starting from the equation 1 the number of coincidences measured by the apparatus can be calculated as

N(ϑ,t)

N₀ e^−λt ·W(ϑ)

N(ϑ,t)

N₀ e^−λt ·(1 + A₂₂P₂(cosϑ) + A₄₄P₄(cosϑ) )

where N₀ is the total counting rate, λ the decay constant and the rest term describes the anisotropic emission probability. If the coefficient A₄₄ is much smaller than A₂₂ (A₄₄ << A₂₂) it is sufficient to determine the angular correlation at two fixed angles ϑ. Usually one uses the angles 90° and 180° because for this angles the Legendre polynomials assume extremely simple values (P₂(cos90°)=−[1/2] and P₂(cos180°)=1). Now to eliminate the exponential decay, which does not contain any information about the modulation, the ratio

R(t) : = 2 ·

N(180°,t) − N(90°,t)

N(180°,t) + 2N(90°,t)

(13)

is defined. Supposed the decay is not perturbed by external magnetic or electric fields, then the ratio R(t) is constant in time and equal to the coefficient A₂₂.

Footnotes:

¹1 erg=10⁻⁷ J and 1 G=10⁻⁴ T (G = Gauss)

Other sites with illustrations to PAC...

Here some useful links to sites, where you can find more or less detailed explanations about the PAC method.

International Website for perturbed angular correlation (PAC)
This is a PAC-Wiki-Site where you can find informations about perturbed angular correlation and where you can add yourself a new contribution.
Perturbed Angular Correlation (PAC) (Saarbrücken)
(Englisch)
Perturbed Angular Correlation Spectroscopy (Leuven, Belgien)
(Englisch)
TDPAC (Leipzig)
(Englisch)
TDPAC (USA)
(Englisch)